Origem do nome
Phi, tem este nome em homenagem ao arquiteto grego Phidias, construtor do Parthenon e que utilizou o número de ouro em muitas de suas obras. É matéria de estudos dos Martinistas, pois leva à compreensão do Livro da Natureza, um dos Livros Martinistas.

A Proporção Áurea ou Número de Ouro ou Número Áureo é uma constante real algébrica irracional. Número tal, que há muito tempo é empregado na arte. Também é chamada de: razão áurea, razão de ouro, divina proporção, proporção em extrema razão, divisão de extrema razão.

Muito frequente é a sua utilização em pinturas renascentistas, como as do mestre Giotto. Este número está envolvido com a natureza do crescimento. Phi (não confundir com o número Pi (p), quociente da divisão do comprimento de uma circunferência pela medida do seu respectivo diâmetro), como é chamado o número de ouro, pode ser encontrado na proporção em conchas (o nautilus, por exemplo), seres humanos (o tamanho das falanges, ossos dos dedos, por exemplo), até na relação dos machos e fêmeas de qualquer colméia do mundo, e em inúmeros outros exemplos que envolvem a ordem do crescimento.

Justamente por estar envolvido no crescimento, este número se torna tão freqüente. E justamente por haver esta freqüência, o número de ouro ganhou um status de "quase mágico", sendo alvo de pesquisadores, artistas e escritores. Apesar deste status, o número de ouro é apenas o que é devido aos contextos em que está inserido: está envolvido em crescimentos biológicos, por exemplo. O fato de ser encontrado através de desenvolvimento matemático é que o torna fascinante.

Proporção Áurea na Natureza
Por que esse número é tão apreciado por artistas, arquitetos, projetistas e músicos? Porque a proporção áurea, como o nome sugere, está presente na natureza, no corpo humano e no universo.
Este número, assim como outros, por exemplo o Pi, estão presentes no mundo por uma razão matemática existente na natureza.

Essa seqüência aparece na natureza, no comportamento da refração da luz, dos átomos, do crescimento das plantas, nas espirais das galáxias, dos marfins de elefantes, nas ondas no oceano, furacões, etc.

Cálculo do Número - Demonstração Algébrica

A razão áurea é definida algebricamente como:

A equação da direita mostra que:

o que pode ser substituído na parte esquerda. Temos, assim:

Cancelando b em ambos os lados, temos:

Multiplicando ambos os lados por nos dá:

Finalmente, arrumando os termos da equação, encontramos:

, que é uma equação quadrática da forma

, em que

Agora, basta resolver esta equação quadrática. Pela Fórmula de Bháskara:

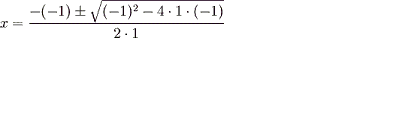
A única solução positiva desta equação quadrática é:

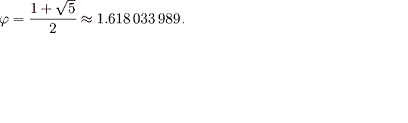
, que é o número